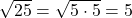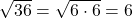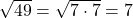Eine (mathematische) Aussage ist eine Behauptung, von der eindeutig feststeht, ob sie wahr oder falsch ist. Eine Aussage im mathematischen Sinne hat also immer einen eindeutigen Wahrheitswert „wahr“ (kurz w) oder „falsch“ (kurz f).


Nicht alles, was gezählt werden kann, zählt.
Albert Einstein (1879 – 1955)
Schnelles Wurzelziehen
Versuch doch mal folgende Aufgabe im Kopf zu berechnen:
Quadratwurzel aus 75076 = ?
Das ziehen einer Wurzel ist eine komplexe Rechenaufgabe. Das können die wenigsten Menschen ohne einen Taschenrechner lösen. Die Kopfrechenmeister machen das sogar im Kopf.
Wenn jemand von Wurzel ziehen spricht ist üblicherweise die Quadratwurzel gemeint. Also die zweite Wurzel wird Quadratwurzel genannt. Eine Wurzel ist eine umgedrehte Potenz. Wenn wir die 2. Potenz von 9 nehmen ist das 9 hoch 2 oder auch 9*9 = 81. Wenn wir dann die Wurzel von 81 ziehen wollen ist das wieder die 9. Das ist die 2. Potenz oder die Quadratwurzel. Als Übersicht hier de Potenzen von 1-32.

Wenn du dir die Ergebnisse ansiehst kannst du feststellen, daß die Potenz von 1 und 9 immer mit 1 Endet. Die Potenz von 2 & 8 immer auf 4, die Potenz von 3 & 7 immer auf 9 und die Potenz von 4 & 6 immer auf 6 Endet. Die Potenz von 5 auf 5 und die vom x0 auf 0. Das ist für das weiter vorgehen wichtig.
 |
Was bedeutet Wurzelziehen?
Eine Wurzel besteht aus folgenden Bausteinen.
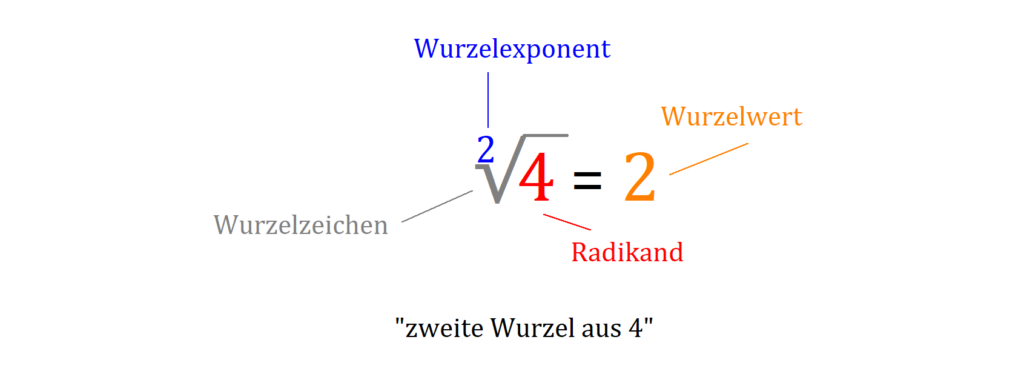
Beim Wurzelziehen mit dem Wurzelexponenten 2 machst du im Prinzip einfach das Quadrieren rückgängig. Wenn du die Zahl 2 quadrierst, erhältst du 4.
2² = 2 ⋅ 2 = 4
Ziehst du die Wurzel aus 4, dann erhältst du wieder die 2.
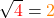
Hinweis: Bei der Quadratwurzel wird meistens der Wurzelexponent 2 nicht mit aufgeschrieben (![\sqrt[\textcolor{blue}{2}]{\textcolor{red}{4}}=\sqrt{\textcolor{red}{4}}](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-50c7cfa5242b1de110a24d9f6736c0e0_l3.png) ). Das Wurzelziehen nennt man auch Radizieren.
). Das Wurzelziehen nennt man auch Radizieren.
Wurzelberechnung Quadratwurzel
Wurzel ziehen geht oft ganz einfach im Kopf. Schauen wir uns die Wurzelberechnung einmal an einem Beispiel an.
Beispiel 1
Du sollst die Wurzel aus 16 ziehen.
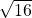
Dazu überlegst du dir, welche Zahl du mit sich selbst malnehmen kannst, sodass 16 herauskommt. Wenn dir die Zahl nicht direkt einfällt, kannst du auch einfach ein paar Zahlen ausprobieren.
2² = 2 ⋅ 2 = 4 ≠ 16
3² = 3 ⋅ 3 = 9 ≠ 16
4² = 4 ⋅ 4 = 16
Da 4 im Quadrat 16 ergibt, ist die Wurzel aus 16 die Zahl 4.
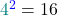
![Rendered by QuickLaTeX.com \sqrt{16} = \sqrt[\textcolor{blue}{2}]{16} = \sqrt[\textcolor{blue}{2}]{4\cdot 4} = \textcolor{teal}{4}](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-9ff201d29f81d7fc975b977fc009d796_l3.png)
Weitere Beispiele
Beispiel 2
Du sollst die Wurzel aus 196 ziehen.

1.Zerlege den Radikanden 196 in Primfaktoren
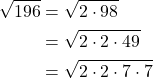
2. Fasse gleiche Faktoren in Potenzen zusammen
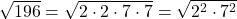
3. Schreibe jeden Faktor unter eine eigene Wurzel
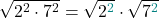
4. Schreibe die Wurzeln als Potenz
![Rendered by QuickLaTeX.com \sqrt[\textcolor{blue}{2}]{2^{\textcolor{teal}{2}}} = 2^{\frac{\textcolor{teal}{2}}{\textcolor{blue}{2}}} = 2^{1} = 2](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-4ef06476e70873231fe79c8cd1bb285b_l3.png)
![Rendered by QuickLaTeX.com \sqrt[\textcolor{blue}{2}]{7^{\textcolor{teal}{2}}}= 7^{\frac{\textcolor{teal}{2}}{\textcolor{blue}{2}}} = 7^{1} = 7](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-57f17a521696a5903be66e13c2cba28e_l3.png)
→ ![\sqrt[2]{2^{2}} \cdot \sqrt[2]{7^{2}} = 2 \cdot 7](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-dfd95b7bae36cefba36f61fba99c83d5_l3.png)
5. Ergebnis der Wurzel berechnen
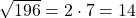
Weitere Beispiele
![Rendered by QuickLaTeX.com \sqrt{256} = \sqrt[\textcolor{blue}{2}]{2^{\textcolor{teal}{8}}} = 2^{\frac{\textcolor{teal}{8}}{\textcolor{blue}{2}}} = 2^{\frac{4}{1}} = 2^{4} = 16](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-500ce5481510b6bb11f28802f668db8a_l3.png)
![Rendered by QuickLaTeX.com \sqrt{144} = \sqrt[\textcolor{blue}{2}]{2^{\textcolor{teal}{4}} \cdot 3^{\textcolor{teal}{2}}} = \sqrt[\textcolor{blue}{2}]{2^{\textcolor{teal}{4}}} \cdot \sqrt[\textcolor{blue}{2}]{3^{\textcolor{teal}{2}}} = 2^{\frac{\textcolor{teal}{4}}{\textcolor{blue}{2}}} \cdot 3^{\frac{\textcolor{teal}{2}}{\textcolor{blue}{2}}} = 2^{2} \cdot 3 = 4 \cdot 3 = 12](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-f7292402f4aca477dc71949cde072c38_l3.png)
Achtung: Bei der Wurzelberechnung kannst du aus negativen Zahlen keine Wurzel ziehen.